Econet Wireless recently announced Zimbabwe as the first commercial site for its highly acclaimed solar powered ‘Home Power Station’ (HPS), this according to a report on the mobile phone company’s website. The announcement is welcome news in a country characterised by chronic load shedding and power failures. Econet’s Corporate Communications Manager Ranga Mberi confirmed to Techzim that the company was launching the product in Zimbabwe initially on a commercial trial period and would in due course provide more information. So does the launch promise a brighter future for Zimbabwean electricity consumers?
Well lets start with the unit itself. The Home Power Station is a device that contains a typical Econet mobile SIM card enabling the device to link up with the cellular network, making it possible for the customer to pre-pay for energy usage, in the same way mobile phone users currently pay for airtime on their cell phone. Connected to the unit are batteries, a 4 light system with 4 switches for each light, a solar panel which goes onto the roof and generates that power for the batteries. The device also features a socket for charging your mobile phone and compatible to the GSM network.
Econet Solar is targeting Africa’s 500 million off the electric grid population. Econet Wireless Group Executive Chairman Strive Masiyiwa in 2011 explained the motivation behind the device was prompted by the lack of “electrical power in major parts of the continent (Africa) or there is massive power deficits, so people get power cuts or the power supply is not reliable…what we are trying to do is to get people to think differently about where power comes from. We have all been raised to think that power comes from one big central power station which then feeds power to homes and industries through a grid. What we are trying to do is to break that down and say the power station can be in your home. So the Home Power Station is a solar powered power station, a little power unit that provides lighting and energy for your home”
There are two issues that can be raised about the HPS. Firstly pricing, both of the unit and the power. The pricing of the unit and the financial model employed is analogous to the contract phone model. As Econet Solar CEO Marco Signorini has noted “the financial model is a subsidy model, just like a mobile phone you don’t pay for the unit upfront you take an agreement or contract with us.”
This is an interesting analogy and on the face of it makes sense. There is however a difference between the phone and HPS unit models. Phones are trendy consumer devices and the HPS is an appliance that you basically put in the background and largely forget about. So a fundamental driver of phone sales is the constant need or more accurately desire to upgrade one’s phone so as to have the latest trendy gadget or to take advantage of new technical features
So for a mobile phone network consumer behaviour in constantly buying and upgrading phones is a major profit driver. In Zimbabwe, though most phones are not bought using this model. Signorini hints at the financial sweetspot by noting that the device converts airtime minutes into energy, this therefore offers the company a potentially infinite (time wise) revenue stream.
As novel as Econet Solar’s technology is the key question will be how it fares against it’s direct competition in the form of solar panel and inverter system which is readily available. The prices of a solar panel system from a local retailer are as follows:
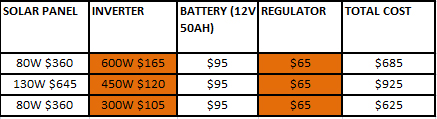
The real innovation that Econet Solar is providing is financial as the consumer now has an option to obtain an energy system without making a significant upfront payment as shown in the table. An additional benefit noted by Signorini is that installing the HPS unit is basically DIY, whereas with other systems one tends to require some expert assistance to install.
Econet Solar have conducted their first trials in South Africa (KwaZulu Natal province) and it’s interesting to note that the country has conducted some interesting public policy experiments of providing electric power to poor households. One such program is the Free Basic Electricity (FBE) scheme which offers 50 kilowatt hours per month for free to most households that have access to electricity. The 50 kwh monthly was set to cover the electricity necessary for basic lighting, a small black-and-white television, a small radio, basic ironing and boiling of water using an electric kettle.
The Energy Modeling Group of the Energy Research Centre (ERC) at the University of Cape Town has conducted several studies about power usage among the poor in places like Khayelitsha township (Cape Town). The Energy Modelling Group found significant uptake of the FBE program by low income households. The Energy Modelling Group cites surveys of energy budgets in extremely poor electrified households that show that these households use power sparingly, typically 20kwh per month when they have to pay for electricity. In this environment electricity is more expensive than traditional alternatives such as coal or firewood for cooking and heating so the rational household watches this budgetary item like a hawk.
Low income households also proportionally use more power for heating water and cooking which they compliment with Liquefied Petroleum Gas (LPG) or paraffin/kerosene. In such a scenario the HPS would represents one solution in a portfolio of applications in providing a comprehensive power solution to low income or off grid households. In Zimbabwe though, at some point every household is off grid, so this product’s appeal will extend beyond the low income base. Its use in an urban setting is bound to be for households that can afford a generator/ invertor or solar/inverter system, but would not be redundant for those who cannot.

26 comments
Inverters are notorious for failing after a year or so, would be nice to know how high a quality these devices are, for $1000 a pop its not a small investment. Also, would be good to know if there are any guarantees?
Yeah we did present those questions to Econet…once we know we shall update
All that gizmo just to power lights…Waste of time
A heating solution would serve people better.
i will wait for the pricing of the thing, but i have my doubt on the success it will have. What would be the benefits of the home station versus setting up your own solar system. I think this might be a hit and miss for Econet.
Please help me guys, there is something I have been missing with the Econet Solar Innovation for sometime. If I get my own solar panels and an invertor for a once off payment I am home and dry to use Solar Energy for Free until the machine lapses. Now what I do not get is paying for Solar Energy. Where will econet be forwarding the payments I made for using their system. Is there any option for me to buy once off their equipment and never pay for use because we are getting the sun for free, no constant treatment, no congestion over the sun, no what ever? Maybe I am lost, this is the 21st century. Please help me here friends.
i think initially you don’t pay anything for the hardware, hence you pay installments monthly i suppose. Which brings into question the pricing of the monthly bills. When i first heard i thought they were setting up solar power plants not these “innovations”. Perhaps when Econet get feedback they will publish more info.
You right the key question will centre around the price of the device vs. a solar panel/ inverter upfront/ over the lifetime of the device. So far Econet are yet to divulge the specific pricing options which we await with baited breath. The pricing model maybe similar to your dstv decoder whose purchasing price is subsidised (In his interview Signorini uses this word), but the obvious difference is that dstv sells you tv content, but Econet Solar are not selling any ‘content’ per se but simply facilitating you to enjoy that ‘content’
I would have preferred Econet had simply built a massive power station than sell us these trinkets.
Personally, i have no desire to pay someone with my airtime or even Ecocash for something i can get for free. I can simply buy my own solar lamps and always put out the solar panel and/battery myself.
If they had invented a gadget which we could put out in the sun to get power and sell the electricity to their mobile network wirelessly i would have been interested.
Anyway, i expect them in the end to go door to door handing out these things because even with advertising, with the little information i have, this thing will not be as ubiquitous as Ecocash.
Environmentally, alot more damage is done when seeking to cook food and not for lighting…at least within the immediate ecosystem.
We use alot of firewood for cooking. That means a tree had to either be cut down or dismembered (pending future destruction).
Most of us grew up reading books and articles on biogas, solar cookers and those super efficient stoves.
I think the solar cookers are what would work very well and will go a significant mile in conservation of our trees. Obviously they are most effective in summer. It is also not expensive. With Econet’s size, it wouldnt be as hard to produce a low-cost solar cooker and make a profit to sustain the venture.
This, I wouldnt buy. But the solar lamps idea was good. My parents have one!
I am so totally lost I think, what exactly does this ‘innovation’ which isnt quite innovative do? Is it solar lighting only, or can I power my pc, tv or any other electrical device that uses low voltage? If its just lights, I’ll stick to my rechargeable lamps thanks, and yes they come with a small solar panel.
If you live in an area with poor or non existent Econet coverage, does it mean you can not use this system? I suppose that the controlling circuitry has mechanisms to detect and report tempering because it seems it would be very easy to bypass the controls with basic tools (like cutting off the solar panel and connecting it to another battery system for example). Econet would need a whole army of employs to follow up on all the units that stopped generating revenue to find out the reason (tempering, fault or no network). Some rough calculations: Under very good solar conditions a 100W unit would generate maybe 1kWh of electricity per day. If they will charge say 20c/kWh (compare to ZESA 15c/kWh) that comes to $6/month. It would take 100 months (8 years) to generate $600 if the unit will operate under peak conditions everyday and all the power generated is used. Hopefully there will be no breakdowns and the cost of mass producing the units is dirt cheap for Econet.
Its nice to look at though
The thing is about these comments – they are not written by the people who would benefit from the use of these kind of products. Affordability is the key, if you bring a cheap easy to use device to off grid on net population, that’s a good start
Pricing will be key for this. It is aimed at users who do not have access to enough upfront capital to purchase a solar kit outright. The panel and inverter prices given in the article are misleading. People can go out now and buy a small 4 lighting and phone charging kit for under $150 (with a one year warranty)
[…] in late 2011 with the promise of a commercial launch we expected to have seen by now. At least trials reported to have been taking place last year suggested so too. Hasn’t happened yet ofcourse. And just as we thought there really […]
Quite a well researched post. Quite informative
owners of the technology/devices; http://solarway.com/
[…] Econet Solar’s home power station. Some thoughts […]
There are similar systems that you can buy for between USD60 and USD160 and you dont have to pay instalments. And some even have two year guarantees
[…] works exactly as the Econet product called Home Power Station, which was introduced back in 2012, but is somehow still not visible at all on the market. One […]
[…] works exactly as the Econet product called Home Power Station, which was introduced back in 2012, but is somehow still not visible at all on the market. One […]
[…] When Econet first entered the energy space, it introduced a number of solar powered products that included lamps, solar powered candles and the Home Power Station (HPS). […]
[…] was retailing at $163 before the discounts) is a different version from the older units that were first introduced when Econet launched its solar devices unit. It also does not have a SIM card […]
i would like to purchase one from my home, how much is it and how do i go about it?
[…] Earlier today the operator announced, on social media, a clearance sale for the HPS which will see the price being reduced by $50 to $49. The offer is valid while stocks last and it becomes the third price reduction for the Power Station since it was first introduced by Econet in 2012. […]