Last month the RBZ’s Monetary Policy Statement revealed that the date for ZimSwitch becoming the National Switch was the 30th of September. That date was an extension for the previous date set which was the 15th of August. The initial date that was set was a little ambitious because the integration that the RBZ required of EcoCash and other mobile money operators was very complicated.
Well, the final deadline has passed and it appears that EcoCash was able to get it over the line. If you dial *151# under “Send Money” (Option 1) you will see an option that says “Send to Account” (Option 5) and that option reveals all the different accounts that you can now send money to:
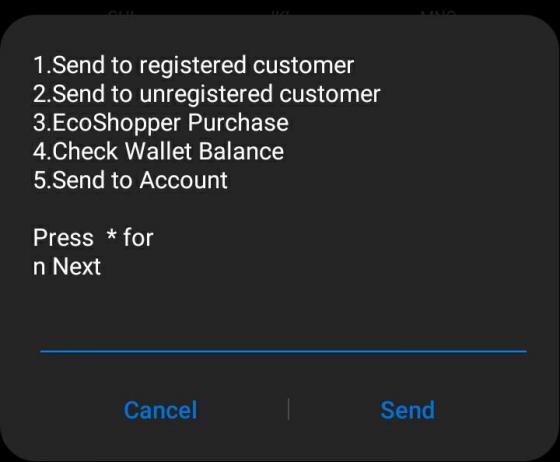
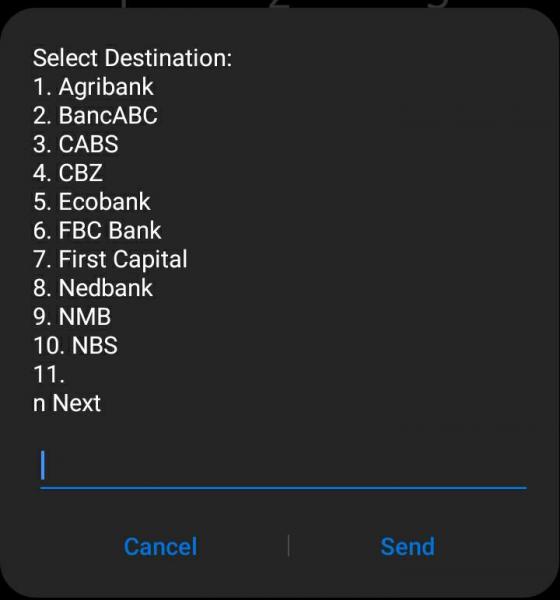
After selecting the bank account or mobile money wallet you want to send to:
- Enter the account number
- Enter the amount
- The reference for the transfer
- Confirm transaction
On the EcoCash App
On the EcoCash mobile app there is an option at the top right corner that says “Send to Account”:
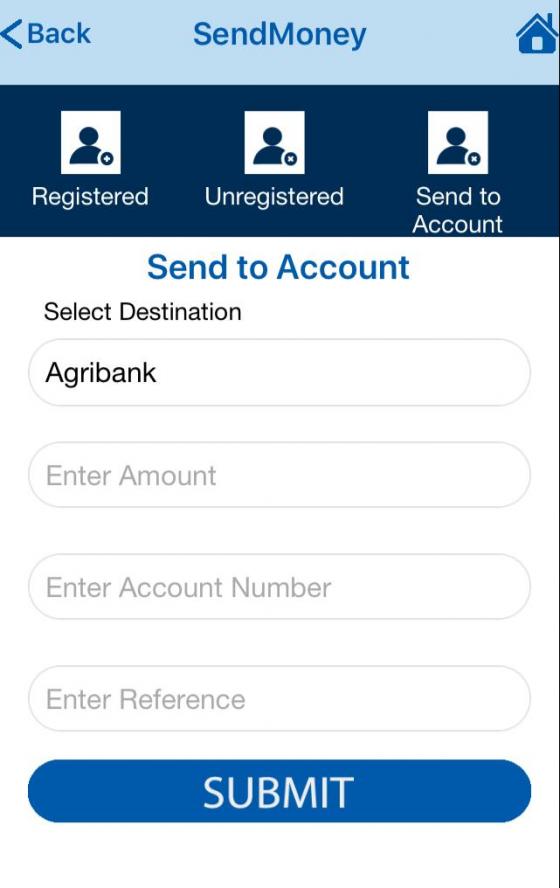
You can then scroll through all the accounts and mobile money wallets and select the one you want.
Throughout the early morning, we have been trying to send money from EcoCash to OneMoney as well as Bank Accounts. On both platforms USSD and mobile app, we are yet to complete a transaction. On USSD the error message is “Invalid MMI error” and on EcoCash’s mobile app the transaction is saying failed.
Errors are coming up in attempts to other mobile money as well as sending money to bank accounts.
22 comments
I just managed. The charges will deter you. I had 161 in my ecocash and transferred 20 to one money. My balance is now 93. Imagine
Vanoda kudimburwa muswe vanhu veEconet. What kind of charges idzodzo. Let’s hope the powers that be are seeing this.
ma charges e zimswitch not econet
I think it’s standard. I used NMB and their ZIPIT transfers are charged at 1% minimum 50, so it’s only economical when trading at high values. Add on the Mthuli 2% ma one
What about from Onemoney to ecocash? Can we have an article on that also.
Very True
I just managed. The charges will deter you. I had 161 in my ecocash and transferred 20 to one money. My balance is now 93. Imagine 48 dollars charge
Yaah its good but charges are heavy. i had 365 in my account and i send 30 to my Onemoney and my balance became 287.5 meaning charges are 48
Sounds good but charges may go up with amount you send
Great odea but charges are heavy. i had 400 in my account and i send 65 to my Onemoney and my balance became 322.5 meaning charges are 48
Charges are massive. i had 90 in my account and i send 30 to my Onemoney and my balance became 12 meaning charges are 48
Chirungu but u no sang a na navo. Kkkk
Who is to benefit after these hefty charges? It’s even worse than when the mobile money accounts were independent.
Econet and Masiiwa are scammers.
I feel like this is for volume transfer, munhu unga itewo 30 dollars isinga kwani ka kombi zupco zvako…
Iyo ecocash yacho will it be able to receive money from banks and what’s the limit
Can you please also write an article that Banks are yet to add Ecocash on their ZIPIT Transfer options.
How can l send 20 dollars and be charged 48 dollars for the transfer? That’s ridiculous
why would one be sending 20 dollars isina zvainoita in the bank account , one doesnt want to swipe some che20 rtgs but wants to send it into the account lets be reasonable the charges are fair 48 dollars for anything less than a 1000
Why are people complaining, Zim Switch isn’t offering this transaction for free, the minister should have just built a government SWITCH to allow the transaction costs to be covered by taxes.
They just went and enriched a privately owned company and forced one money, ecocash and telecash to fund another private organization at the expense of us the people.
No when you transact from ecocash to one money you pay Zim Switch, Ecocash and One money not forgetting the 2% for Ncube. So yes transfer 30 bucks you will pay 43 for the transaction.
Dont just go complaining about Ecocash without getting the facts straight, there is a reason why they stuck to wallet to bank cause they could control the costs to benefit you the customer. Zim Switch won’t make this cheap because they want to push their own agenda, they already giving out merchant codes, and they should cause they’re are private business.
Is there anyone who did a transfer of $1000 and above so that we can compare the charges or see if it increase from the $48 pegged on little amounts.
These pple vakutsvaga mari nedemo gore rino hameno